Capacitance and Capacitors
Capacitance is the ratio of charged gained per potential gained of the conductors. Unit of capacitance is Coulomb per Volt and it is called as Farad (F).
 Capacitance is a scalar quantity. Graph given below shows the relation of a charged gained and potential gained of conductor sphere.
Capacitance is a scalar quantity. Graph given below shows the relation of a charged gained and potential gained of conductor sphere.
 There is a linear relation between gained charge and gained potential. Slope of the graph gives us the capacitance of the sphere.
There is a linear relation between gained charge and gained potential. Slope of the graph gives us the capacitance of the sphere.
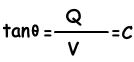 As I said before, farad is the unit of capacitance, however, we commonly use (pF) picofarad=10-¹²F, (µF) microfarad=10-⁶F and (nF) nanofarad=10-⁹F.
As I said before, farad is the unit of capacitance, however, we commonly use (pF) picofarad=10-¹²F, (µF) microfarad=10-⁶F and (nF) nanofarad=10-⁹F.
Sphere having radius r and charge q has capacitance;
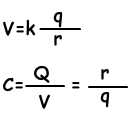 Capacitors
Capacitors
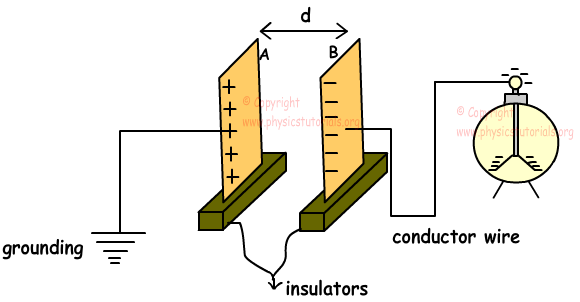
Capacitors are devices designed for storing charge. They are commonly used in computers or electronic systems. They consist of two conductor plates located with a distance to each other. They do not touch each other. When we connect the negatively charged plate with neutral sphere, they share total charge until the potentials become equal and leaves of the electroscope rises. Then we locate plate A with a distance d to B. Since we ground the plate it is neutral at the beginning. Since B is negatively charged it affects the plate A and it is positively charged by induction. If we put different insulator material between the plates like plastic the leaves of electroscope are a little bit closed. We can conclude that, capacitance of the plates depends on the distance between the plates.
 In a circuit we represent the capacitor with the symbol;
In a circuit we represent the capacitor with the symbol;
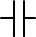 And battery which supplies potential difference is represented by the symbol;
And battery which supplies potential difference is represented by the symbol;
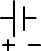 We show capacitors and battery in circuit as given below;
We show capacitors and battery in circuit as given below;
 Capacitance of a plate depends on;
Capacitance of a plate depends on;
Area of the plates
Distance between the plates d
Dielectric constant between the plates ε₀ The capacitance of the plates is found with the following formula;
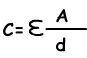 Dielectric constant between the plates ε₀ depends on the type of material. For example, vacuum has ε=8, 85.10-¹² F/m and water has ε=717.10-¹²F/m.
Dielectric constant between the plates ε₀ depends on the type of material. For example, vacuum has ε=8, 85.10-¹² F/m and water has ε=717.10-¹²F/m.
Example: Calculate the capacitance of the capacitor having dimensions, 30 cm X 40 cm and separated with a distance d=8mm air gap.
A=30.10-²mX40.10-²m=0,12m²
C=(8, 85.10-12C2/N.m²).0,12m²/8.10-³m
C=0,13275.10-⁹ F