Direction of Wave Propagation
If we know shape of the pulse at an instant time, or propagation direction of the particles of the pulse we can find the direction of wave propagation.
 Example: Given picture below shows the direction of wave propagation. Find the directions of the vibration at points A, B and C.
Example: Given picture below shows the direction of wave propagation. Find the directions of the vibration at points A, B and C.
 We draw the shape of the pulse after t s and find the directions of the vibration at points A, B and C.
We draw the shape of the pulse after t s and find the directions of the vibration at points A, B and C.
 Velocity of the Spring Pulse
Velocity of the Spring Pulse
Distance taken at an instant time by the pulse is called velocity of the pulse. Velocity of the spring pulse depends on force exerted on the spring and spring constant µ. Spring constant depends on the type of the spring; it is found by the following formula;
µ=mass/length
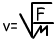 Where; v velocity of the spring pulse (m/s),
Where; v velocity of the spring pulse (m/s),
µ is the spring constant (kg/m), and F is the force exerted on the spring (N).
 Example: Find relation of propagation velocity of pulses of identical springs in given picture below.
Example: Find relation of propagation velocity of pulses of identical springs in given picture below.
 Force exerted on the springs directly proportional to the hanged masses. Thus, since G₃>G₂>G₁,
Force exerted on the springs directly proportional to the hanged masses. Thus, since G₃>G₂>G₁,
v₃>v₂>v₁.
Example: There are three identical springs having equal masses and different lengths L₃>L₂>L₁. Find the relation of velocities of pulses.
 Propagation velocity of the pulse is;
Propagation velocity of the pulse is;
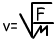 Spring constant is;
Spring constant is;
µ=mass/length
Relation of the lengths,
L₃>L₂>L₁
Relation of the spring constants;
µ₃<µ₂<µ₁
Propagation velocities become;
v₃>v₂>v₁