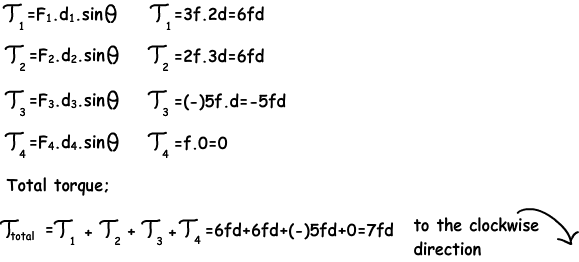Torque
We define torque as the capability of rotating objects around a fixed axis. In other words, it is the multiplication of force and the shortest distance between application point of force and the fixed axis. From the definition, you can also infer that, torque is a vector quantity both having direction and magnitude. However, since it is rotating around a fixed axis its direction can be clockwise or counterclockwise. During the explanations and examples we give the direction “+” if it rotates clockwise direction and “-” if it rotates counterclockwise direction. Torque is shown in physics with the symbol “τ”. You can come across torque with other name “moment”. Now, we examine given pictures one by one to understand torque in detail.
How can we find the shortest distance between the applied force and fixed axis?
All you know that, shortest distance between two points is the straight line connecting them. In this situation distance connecting these two points is the length of the object. Direction of the torque is “+” because force rotates the object in clockwise direction. (We ignore the weight of the object in all situations given below.)
Thus, we can write the torque equation like;
Τ=Applied Force.Distance
In this picture, we have a different situation where the object is fixed to the wall with an angle to the horizontal. Direction of the torque in this situation is “-” because force rotates the object in counterclockwise direction. As we said before we need shortest distance between the force and turning point. Dashed line in the picture shows this distance which can be found by using trigonometry and final equation of torque becomes;
Τ=Applied Force.Distance.sinΘ
Final situation shows that, if the extension of the force is passing on the rotation axis then what would be the torque?
I want to explain this situation by giving other example. Think that you are opening a door. If you push the door as in the case of given picture above, the door does not move. However, if you apply a force to the door like in the first and second situations given above the door is opened or closed. What I try to say is, if the force is applied to the turning point then it does not rotate the object and there won’t be torque.
Example: If the given triangle plate is fixed from the point O and can rotate around this point, find the total torque applied by the given forces.
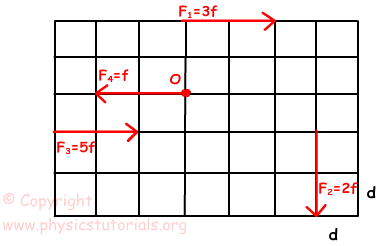
Example: If the plate is fixed from the point O, find the net torque of the given forces.
