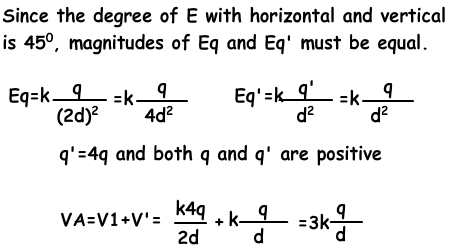Electric Potential and Electric Potential Energy
We learned that in work power energy chapter, objects have potential energy because of their positions. In this case charge in an electric field has also potential energy because of its positions. Since there is a force on the charge and it does work against to this force we can say that it must have energy for doing work. In other words, we can say that Energy required increasing the distance between two charges to infinity or vice verse. Electric potential energy is a scalar quantity and Joule is the unit of it. We use following formula to find the magnitude of EP;
 Be careful!
Be careful!
- In this formula if the charges have opposite sign then, Ep becomes negative, if they are same type of charge then, Ep becomes positive.
- If Ep is positive then, electric potential energy is inversely proportional to the distance d.
- If Ep is negative then, electric potential energy is directly proportional to the distance d.
 In Figure 1 and Figure 2, charges repel each other, thus external forces does work for decreasing the distance between them. On the contrary, in Figure3, charges attract each other, distance between them is decreased by electric forces, and there is no need for other external forces.
In Figure 1 and Figure 2, charges repel each other, thus external forces does work for decreasing the distance between them. On the contrary, in Figure3, charges attract each other, distance between them is decreased by electric forces, and there is no need for other external forces.
Example: System given below is composed of the charges, 10q, 8q and -5q. Find the total electric potential energy of the system.

 Electric Potential
Electric Potential
Electric potential is the electric potential energy per unit charge. It is known as voltage in general, represented by V and has unit volt (joule/C).
 1C charge is brought to the point A from infinity. Work done here is called potential of q at A. Electric potential is found by the given formula;
1C charge is brought to the point A from infinity. Work done here is called potential of q at A. Electric potential is found by the given formula;
V=k.q/d
V is a scalar quantity. If q is negative then V becomes negative, or if q is positive then V becomes positive.
Surfaces having equal potentials are called equipotential surfaces.
Potential of a Charged Sphere
Potential at surface is equal to the potential inside the sphere. Since there is no force acting inside the sphere, work is not done to bring the charge from surface to the inside of the sphere. As the distance from the surface of the sphere increase, potential decreases. Picture given below shows the change in the potential of the sphere inside, surface and outside. As you can see, potential is constant inside and surface of the sphere; however, it decreases with the increasing distance outside it.
 Potential Difference between Two Points
Potential Difference between Two Points
Work done against to the electric field to move unit charge from one point to another is called potential difference between these two points. This difference is found by differences of potential of last point from initial point. If we take the point charge from A to B, then potential difference is found by the formula;
 Example: Find the potential difference between points A and B, VAB in terms of kq/r?
Example: Find the potential difference between points A and B, VAB in terms of kq/r?

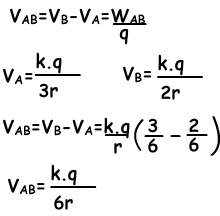 Example: If the total electric field produced by q and q’ is like in the picture given below, find the electric potential of the A.
Example: If the total electric field produced by q and q’ is like in the picture given below, find the electric potential of the A.