Motion With Graphs With Examples
DESCRIBING MOTION WITH GRAPHS
Position vs. Time Graphs: Graphs are commonly used in physics. They give us much information about the concepts and we can infer many things. Let’s talk about this position vs. time graph.
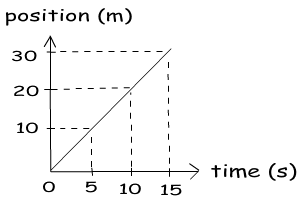 As you see on the graph, X axis shows us time and Y axis shows position. We observe that position is linearly increasing in positive direction with the time. We understand from this linear increasing, our velocity is constant. If it was not constant we would see a curved line in our graph. Now, we use this graph and make some calculations.
As you see on the graph, X axis shows us time and Y axis shows position. We observe that position is linearly increasing in positive direction with the time. We understand from this linear increasing, our velocity is constant. If it was not constant we would see a curved line in our graph. Now, we use this graph and make some calculations.
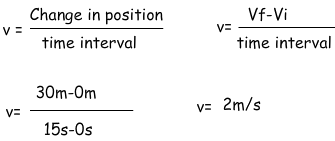 From the given graph we calculate velocity; there is another way of this calculation. We just look at the slope of the graph and find the velocity. What we mean by slope is;
From the given graph we calculate velocity; there is another way of this calculation. We just look at the slope of the graph and find the velocity. What we mean by slope is;
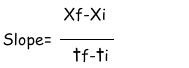 which is the equation we use in calculation of the velocity.
which is the equation we use in calculation of the velocity.Position is increasing positive direction.
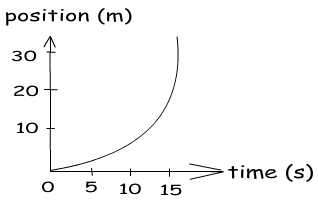 In this graph our velocity is changing. As a result of this change graph has curved line not linear. So position does not increase linearly. We can also find the velocity of the object from this graph. We should first find the slope of the curve and calculate the velocity.
In this graph our velocity is changing. As a result of this change graph has curved line not linear. So position does not increase linearly. We can also find the velocity of the object from this graph. We should first find the slope of the curve and calculate the velocity.
Example: Using the given graph find the velocity of the object in intervals (1s – 3s) and (3s – 5s).
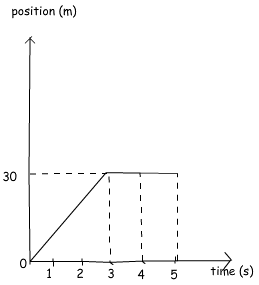
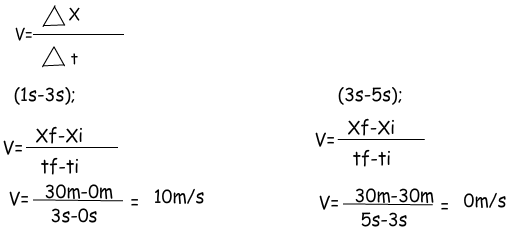 In graph problems you should be careful while reading it. For example, in this example in the interval (3s-5s) position does not change. You can easily see it from the graph, but I want to show the calculation of this and it gives us same result. If there is no change in position then there is no velocity or vice versa. You can say more things about the motion of the object by just looking of the graph. The important thing is that you must know the relations, meaning of the slopes or area of the graphs. We will solve more examples using graph for deep understanding and analyzing the motion from the graphs.
In graph problems you should be careful while reading it. For example, in this example in the interval (3s-5s) position does not change. You can easily see it from the graph, but I want to show the calculation of this and it gives us same result. If there is no change in position then there is no velocity or vice versa. You can say more things about the motion of the object by just looking of the graph. The important thing is that you must know the relations, meaning of the slopes or area of the graphs. We will solve more examples using graph for deep understanding and analyzing the motion from the graphs.
This position time graph is an example of increasing position in negative direction. Red line shows nonlinear increasing and black line shows linear increasing. We say that linear increasing in position is the result of constant velocity which means zero acceleration. Moreover, nonlinear increase in the position is the result of changing velocity and it shows there is a nonzero acceleration.

Until now we saw graphics including speeding up motion in positive and negative directions. Now we talk about a little bit slowing down object’s graphs.
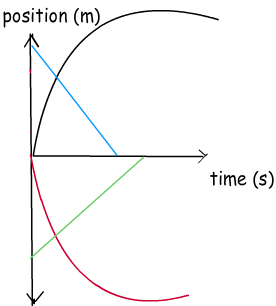 For example, in this given graph, our position is decreasing in different directions. Red line shows the position of the object which is slowing down in negative direction and black line shows the position of the object slowing down in positive direction. However, the blue and green lines show the linear decrease in position in positive and negative directions.
We have seen various type of position vs. time graphs. I think they will help you in solving problems. It is really easy, you should just keep in mind that “slope shows the velocity”.
Velocity vs. Time Graphs
In velocity vs. time graphs, x axis is time as in the case of position vs. time graphs and y axis is velocity. We can benefit from this graph by two ways. One of them is area under the graph which gives the displacement and the slope which gives the acceleration.
For example, in this given graph, our position is decreasing in different directions. Red line shows the position of the object which is slowing down in negative direction and black line shows the position of the object slowing down in positive direction. However, the blue and green lines show the linear decrease in position in positive and negative directions.
We have seen various type of position vs. time graphs. I think they will help you in solving problems. It is really easy, you should just keep in mind that “slope shows the velocity”.
Velocity vs. Time Graphs
In velocity vs. time graphs, x axis is time as in the case of position vs. time graphs and y axis is velocity. We can benefit from this graph by two ways. One of them is area under the graph which gives the displacement and the slope which gives the acceleration.We have talked about different kinds of motion such as, constant motion having constant velocity, accelerated motion like speeding up or slowing down. For instance, in this graph as it seen our velocity is constant, time passes but velocity does not change. What you see when you look at this graph?
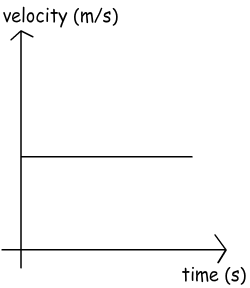 We see the relation of velocity and time, how velocity is changing with time. It can be said for this graph acceleration is zero because there is no change in velocity. Moreover, from velocity vs. time graphs we can calculate displacement of the object. How can we do this? Let’s think together. First, look at the definition of displacement;
We see the relation of velocity and time, how velocity is changing with time. It can be said for this graph acceleration is zero because there is no change in velocity. Moreover, from velocity vs. time graphs we can calculate displacement of the object. How can we do this? Let’s think together. First, look at the definition of displacement;
 Since, the velocity times time gives us displacement the area under the velocity vs. time graph also gives us the displacement of the object. Look at the example given below to understand what we mean by the area under the graph.
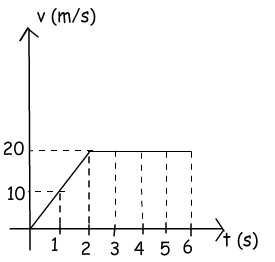
Example: Using the given graph calculate the displacement of the object for the interval (0s – 4s).
Since, the velocity times time gives us displacement the area under the velocity vs. time graph also gives us the displacement of the object. Look at the example given below to understand what we mean by the area under the graph.
Example: Using the given graph calculate the displacement of the object for the interval (0s – 4s).
 To solve this problem, I use the technique given above and classic formula. The area under the graph will give us the displacement. Then we compare the results of two techniques.
To solve this problem, I use the technique given above and classic formula. The area under the graph will give us the displacement. Then we compare the results of two techniques.
 As you can see, the results are the same, thus, we can say that in velocity vs. time graphs we can find the displacement by looking at the area under the graph.
As you can see, the results are the same, thus, we can say that in velocity vs. time graphs we can find the displacement by looking at the area under the graph.In this graph there is a linear increase in velocity with respect to time so, the acceleration of the motion is constant. Moreover, we can also calculate the displacement by looking at under the area of the graph. Let’s solve another example for deep understanding.
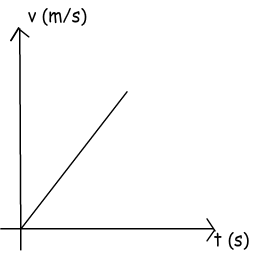 Example: Calculate the displacement of the car from the given graph.
Example: Calculate the displacement of the car from the given graph.
 We can calculate displacement by using the area under the graph, to do this we can first calculate the area of the triangle shown with blue lines and then rectangle shown with red lines. Finally the sum of these two areas gives us the total displacement of the car.
We can calculate displacement by using the area under the graph, to do this we can first calculate the area of the triangle shown with blue lines and then rectangle shown with red lines. Finally the sum of these two areas gives us the total displacement of the car.

This graph shows the different accelerated motions. The lines are curved because acceleration is not constant. They represent the decreasing and increasing velocity in positive and negative directions. However, we do not deal with such problems now.
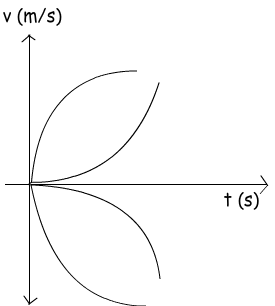 We have discussed the velocity vs. time graphs. When you look at these graphs you can find the displacement and acceleration of the object by looking at the slope for acceleration and area for displacement.
We have discussed the velocity vs. time graphs. When you look at these graphs you can find the displacement and acceleration of the object by looking at the slope for acceleration and area for displacement.