Distance and Displacement with Examples
Distance is a scalar quantity representing the interval between two points. It is just the magnitude of the interval. However, Displacement is a vector quantity and can be defined by using distance concept. It can be defined as distance between the initial point and final point of an object. It must be the shortest interval connecting the initial and final points, that is a straight line.Let’s look at the below examples for deep understanding.
 Look at the picture above, boy travels from D to A, A to B, B to C and C to D. Displacement from D to D (which are our initial and final points) is zero. However, distance traveled is not zero. It is equal to the perimeter of the rectangle.
Look at the picture above, boy travels from D to A, A to B, B to C and C to D. Displacement from D to D (which are our initial and final points) is zero. However, distance traveled is not zero. It is equal to the perimeter of the rectangle.
Another example of distance and displacement is given below.
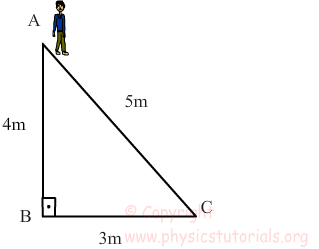 John walks from the point A to B to C. What does the distance he travel? What is the displacement?
John walks from the point A to B to C. What does the distance he travel? What is the displacement?
Let’s calculate first the distance that john travels. While calculating distance, we look at the numeric value of interval between traveled points. As you can see from Figure 1.2 he travels from A to B to C. Distance from A to B is 4m and B to C is 3 m. Their sum will give us total distance;
4+3=7
Then it’s time to calculate displacement. As I mentioned before displacement is a vector quantity.Thus, it must have both magnitude and direction. In this example our initial point is A and our final point is C. Displacement vector is an internal between the initial and final points. As it clearly seen in the Figure1.2 interval between A to C is 5m. So, our displacement vector is 5m and it’s direction is from the point A to C.
Example: Look at the picture given below. An object moves from point A through B, C, D, E and stops at point F.
a) Find final displacement.
b) Find distance taken from point A to D.
 a) We find final displacement by drawing straight line from point A to final point F. As you can see from the graph, object changes its position 8m.
a) We find final displacement by drawing straight line from point A to final point F. As you can see from the graph, object changes its position 8m.
Displacement = Final poisition - Initial position Displacement = 10m - 2m = 8m
b) We find distance taken by object; A to B =10 - 2 = 8m B to C = 10 - 2 = 8m C to D = 10 - 6 = 4m Total distance taken from point A to D is = 8m + 8m + 4m =20m