Work
Suppose that, a force is applied an object and object moves in the direction of applied force then we said work has done. Let me explain in other words. There must be a force applied to an object and object must move in the direction of the applied force. If the motion is not in the direction of force or force is applied to an object but there is no motion then we cannot talk about work. Now we formulize what we said above.
Since force is a vector quantity both having magnitude and direction work is also a vector quantity and has same direction with applied force. We will symbolize force as F, and distance as d in formulas and exercises. If there is an angle between force and direction of motion, then we state our formula as given below;
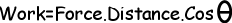
In this case force and distance are in the same direction and angle between them is zero. Thus, cos0 is equal to 1. W=F.d If the force and distance are in opposite directions then angle between them becomes 180 degree and cos180 is equal to -1.
W = -F.d
The last case shows the third situation in which force is applied perpendicularly to the distance. Cos90 degree is zero thus, work has done is also zero. W=F.d.cos90º=0
Now let’s talk about the unit of work. From our formula we found it kg.m²/s² however, instead of this long unit we use joule. In other words;
1 joule = 1N.1m
Look at the given examples below, we will try to clarify work with examples.
Example: 25 N force is applied to a box and box moves 10m. Find the work done by the force. (Sin37º=0,6 and cos37º=0,8)
Since the box moves in X direction, we should find the X and Y components of the applied force. Y component of the force does not responsible for the work. Motion of the box is in X direction. So, we use the X component of the applied force. Since the angle between X component of force and distance is zero cos0º becomes 1. I did not mention it in the solution. If it was a different value than 1 I must write it also.
Example: Look at the given picture below. There is an apple having a force applied perpendicularly on it. However, it moves 5m in X direction. Calculate the work done by the force.
Example: If the box is touching to the wall and a force is applied finds the work done by the force.
Box is touching to the wall and force cannot move it. Because there is no distance we cannot talk about the work. As you can see our formula;
Work=Force. Distance If one of the variables is zero than work has done becomes zero.