Speed and Velocity with Examples
In the last sections we have learned scalar and vector concepts. Beyond the definitions of these concepts we will try to explain speed and velocity terms. As mentioned in last section distance and displacement are different terms. Distance is a scalar quantity and displacement is a vector quantity. In the same way we can categorize speed and velocity. Speed is a scalar quantity with just concerning the magnitude and velocity is a vector quantity that must consider both magnitude and direction.
SPEED
Speed can be defined as “how fast something moves” or it can be explained more scientifically as “the distance covered in a unit of time”. In daily life we use the first definition and say the faster object has higher speed. Speed does not show us the direction of the motion it just gives the magnitude of what distance taken in a given time. In other words it is a scalar quantity. We use a symbol v to show speed. Let me formulate what we talk above;
Speed=distance/time
From the above formula we can say that speed is directly proportional to the distance and inversely proportional to the time. I think it’s time to talk a little bit the units of speed. Motor vehicles commonly use kilometer per hour (km/h) as a unit of speed however in short distances we can use meter per second (m/s) as a unit of speed. In my examples and explanations I will use m/s as a unit.
Example: Calculate the speed of the car that travels 450m in 9 seconds. Speed = Distance / Time Speed = 450m / 9 s = 50 m/s
VELOCITY
Velocity can be defined as “speed having direction”. As you can understand from the definition velocity is a vector quantity having both magnitude and direction. In daily life we use speed and velocity interchangeably but in physics they have different meanings. We can define velocity as the “rate of change of displacement” whereas “the speed is rate of change of distance”. While we calculate speed we look at the total distance, however, in calculating velocity we must consider the direction and in short we can just look at the change in position not the whole distance traveled. If a man walks 5m to east and then 5m to west speed of that man calculated by dividing total distance traveled which is 10m to the time elapsed, however, velocity calculated by dividing the displacement to the elapsed time, which is 0m divided elapsed time gives us zero. In other words, if the displacement is zero we can not talk about the velocity.
Be careful!! There must be a change in the position of the object to have a velocity.
We use ∆ symbol to show the change in something. For example, we can symbolize the change in position as ∆X.
Example: Calculate the speed and velocity of the man moving 45m to the north, and 36m to the south in 27 seconds.
First we should calculate distance traveled and displacement of the man to calculate speed and velocity.
Total distance covered = 45m + 6m = 81m
Speed = total distance/time of travel = 81m / 27s = 3m/s
Velocity = displacement/time = (45-36) m / 27s = 9m /27s = 0,33m/s
We show with this example that speed and velocity are not the same thing.
Average Speed and Instantaneous Speed
A moving object does not have the same speed during its travel. Sometimes it speeds up and sometimes slows down. At a given instant time what we read from the speedometer is instantaneous speed. For example, a car moving with a constant speed travels to another city, it must stop at red lights in the traffic, or it should slow down when unwanted situations occur in the road. At the end of the trip, if we want to learn average speed of the car we divide total distance to total time the trip takes.
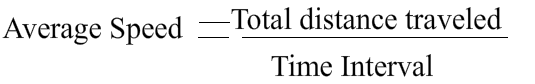Assume that car travels 500 km in a 5 hour. When we calculate the average speed we see that it is 100km/h. Of course the car does not travel with a 100 km/h constant speed. It has many instantaneous speeds and 100 km/h is the average of those instantaneous speeds.
Average Velocity and Instantaneous Velocity
We can follow the same steps used in the definition of average and instantaneous speed while defining average and instantaneous velocity. Instantaneous velocity is the velocity at a given instant of time, however, as in the case of speed, average velocity is calculated with displacement over time interval.
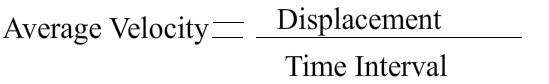Example: A man traveling with his car 150m to the east and than 70m to the west, calculate the average speed and velocity of the car if the travel takes10 seconds.
Average Velocity=Displacement/Time Interval Displacement=150m-70m=80m
Average Velocity= 80m/10s=8m/s east
Average Speed=Total Distance Traveled/Time Interval
Average Speed= (150m+70m)/10s
Average Speed=22m/s
This is a good example which shows the difference of velocity and speed clearly. We must give the direction with velocity since velocity is a vector quantity however, speed is a scalar quantity and we do not consider direction.