Magnetism Exam 1 and Problem Solutions

1. Find the forces exerted by S poles of magnets given below. Magnetism F=k.M₁.M₂/r²=(10⁻⁷.10⁻⁴.10⁻³)/(0,6)²

F=10⁻¹⁴/(36.10⁻²)

F=10⁻¹²/36

2. Find resultant magnetic field at point O, produced by I₁, I₂ and I₃. Magnetism Magnitudes of magnetic fields;

B₁=2k.6/0,1=12.10⁻⁷/10⁻¹=12.10⁻⁶ N/Amps.m

B₂=2k.4/0,1=8.10⁻⁷/10⁻¹=8.10⁻⁶ N/Amps.m

B₃=2k.8/0,1=16.10⁻⁷/10⁻¹=16.10⁻⁶ N/Amps.m Magnetism Bresultant=B₁+B₂+B₃

Bresultant=√(12.10⁻⁶-16.10⁻⁶)²+(8.10⁻⁶)²

Bresultant=4√5.10⁻⁶ N/Amps.m

3. A, B and C wires are given below. Find the magnetic field of A, B and C at points X and Y. Magnetism Directions of magnetic fields at point X are found using right hand rule.

BA: outward

BB:inward

BC:inward

BX=BB+BC-BA

BX=2k.3I/3d+2k.I/d-2k.I/d=2k.I/d

Directions of magnetic fields at point Y are;

BA: inward

BB:inward

BC:outward

BY=BA+BB-BC

BY=2k.I/d+2k.3I/d-2k.I/d=2k.3I/d

Ratio of magnetic fields;

BX/BY=2k.I/d/2k.3I/d=1/3

4. Solenoid having number of loops N and surface area A is shown in picture given below. If we change the position of solenoid as shown in the picture below, find the equation used for finding induced emf of solenoid. Magnetism Induced emf=ε=-(∆Φ)/(∆t).N

Change in Flux;

∆Φ=Φ₂-Φ₁

Φ₁=0, since cross section area of solenoid and magnetic field lines are parallel to each other.

Φ₂=B.A

∆Φ=B.A-0=B.A

ε=-B.A.N/t

5. Draw the directions of magnetic field lines at point A, B, C and D in the picture given below. 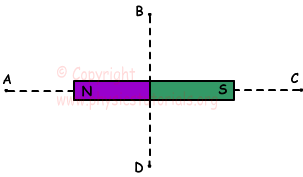Magnetism Directions of magnetic field lines are drawn from N pole to S pole as shown in the picture given below.