Critical Angle and Total Reflection
Look at the given picture. Rays with different angles coming from the source at the bottom of the water filled glass, refracted from the surface, reflected and directly pass to the second medium without any reflection and refraction.
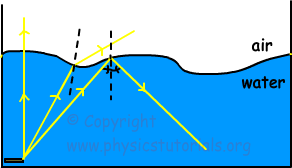In the previous section we learned Snell’s law of refraction. According to this law; reflecting, refracting or directly passing of light to the other medium is depends on angle of incident ray and refractive indexes of the mediums. Here, you see that light coming from the medium having larger refractive index to the smaller refractive index. Thus, light refract away from the normal. According to the angle of incident ray, at one point it does not refract but goes parallel to the boundary of the mediums. We called this angle as critical angle. If the angle of incident ray is larger than the critical angle then it does not refract but it does total reflection. In the picture given above, first light is coming from the normal thus it does not reflect or refract; it passes directly to the second medium. Second light coming with an angle smaller than the critical angle, refracts and passes to the second medium. However, third light coming with an angle larger than the critical angle does total reflection and can not pass to the second medium.
Now we use Snell’s law of refraction and find the equation of critical angle.
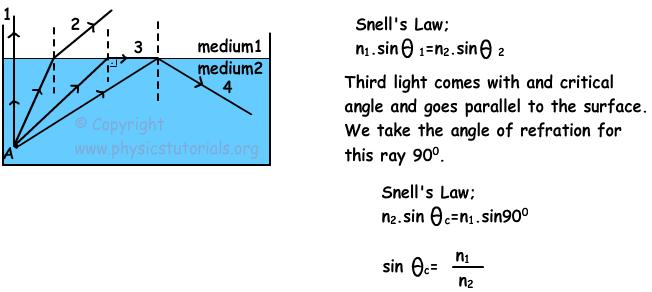Where Θc is critical angle and rays coming with an angle larger than Θc make total reflection.
Example: Refractive indexes of medium A is 2, and medium B is 1,6. Find the critical angle of the rays coming from the medium A to B.
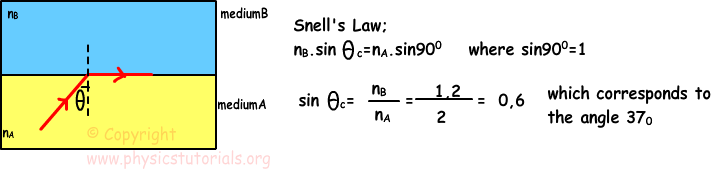Example: Which paths, given in the picture below, can be followed by the light ray A?
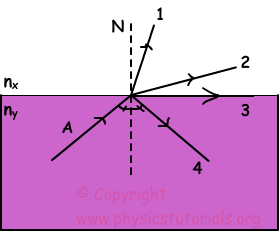We do not know the refractive indexes of the mediums. If the nx is larger than the ny then light ray follows the path shown in 1 it approaches to the normal. On the contrary, if the ny is larger than nx and angle of incident ray is smaller than the critical angle then it follows the path shown in 2. If the angle of incident ray is equal to the critical angle and ny is larger then nx the ray A follows the path shown in 3. Finally, if the angle of incident ray is larger than the critical angle and ny is larger than nx ray follows the path shown in 4 it does total reflection.
Total Reflection in Prisms
Critical angle for glass in air is 42º. Thus, rays coming with an angle 45º, which is larger than the critical angle, to the glass make total reflection.
This prism is used for to change the direction of incident ray 90º. Rays come to the prism perpendicularly and they do not refract, they hit the surface with an angle 45 and make total reflection.
In this prism, rays again make total reflection. This type of prisms is used for to change direction of rays 180º. As you can see rays leave the prism in opposite direction.
This is the last example of prism that I choose for you. In this case direction of light is not changed it goes parallel to the incident ray after making total reflection.
