Kinematics Exam4 and Problem Solutions
1. Look at the given pictures and find which one of the vectors given in the second figure is the relative velocity of A with respect to B.
Since the observer is B, we find relative velocity of A with respect to B with following formula;
VAB=VA-VB
Using vector addition properties we find relative velocity as given figure below.
2. Velocity of the river with respect to ground is 2m/s to the east. Width of the river is 80m. One boat starts its motion on this river at point A with a velocity shown in the figure below. Find the time of the motion and horizontal distance between the arrival point and point A.
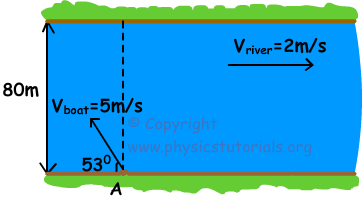Components of boat velocity;
Vx=5.cos530=-3m/s to the west
Vy=5.sin530=4m/s to the north
Time for passing the river is; t=X/V=80m/4m/s=20s
Resultant velocity in horizontal is; VR=VX+Vriver VR=-3+2=-1m/s to the west
Distance taken in horizontal is; X=V.t X=1m/s.20s=20m
3. A river boat in a river having constant velocity travels 120m distance from point A to B in 20 s and turns back from B to A in 12 s. If the velocity of the river is zero, find the time of this trip.
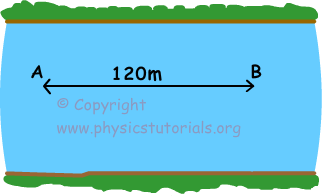Since the time of trip from B to A is longer than the time of trip from A to B, direction of river velocity is to the west.
Velocity of river with respect to ground is Vriver, and velocity of boat with respect to river is Vboatriver.
Velocity of boat with respect to ground when it travels from A to B becomes;
Vb=Vboatriver-Vriver
and when it travels from B to A;
Vb=Vboatriver+Vriver
We can find velocities using following formula;
1.Vboatriver-Vriver=120/20=6m/s
and
2.Vboatriver+Vriver=120/12=10m/s
Solving equations 1. and 2. we find the velocities of river and boat.
Vboatriver=8m/s and Vriver=2m/s
If the velocity of river is zero, boat travels 240m distance in;
240=8m/s.t
t=30s
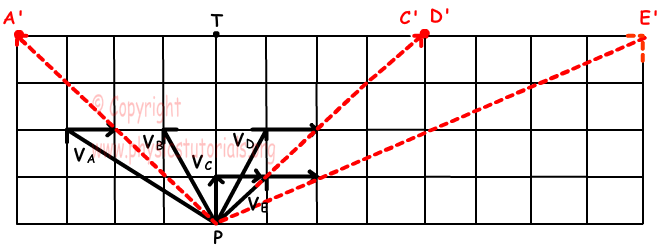
4. Five swimmers start swimming from point P. If the swimmer B passes the river and reaches other side of the river at point T, find the exit points of other swimmers from the river.
Since swimmer B reaches other side of the river at point T, velocity of swimmer B must be in PT direction. We find velocity of river as 1 unit to the east. Picture given below shows the exit points of other swimmers from river.
5. Two swimmer start to swim at the same time as shown in the picture below. If they meet at point C, find the ratio of their velocities with respect to water.
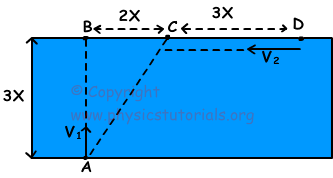If there is no river velocity, swimmer1 reaches point B, and swimmer₂ reaches point B, however, river velocity makes them reach to point C. In other words, swimmer₁ having velocity V₁ takes 3X distance and swimmer2 having velocity V₂ takes 5X distance during same time. Thus;
V₁/V₂=3/5