Force Acting on Moving Particle and Current Carrying Wire
As we learned before, charged particles produce electric field around themselves. In an electric field charged particles are exerted force F=qE. The motion of the charges in an electric field produce current and as a result of the current magnetic field is produced. This magnetic field exerts force on the charged particles inside the field. Experiments done on this subject show that we can find the force exerted on the current carrying wire with following formula; F=B.i.l.sinß
where B is the magnetic field strength, i is the current and l is the length of the wire and ß is the angle between magnetic field and the wire.
We find direction of the force by right hand rule. Picture given below shows the direction of magnetic field current and force;
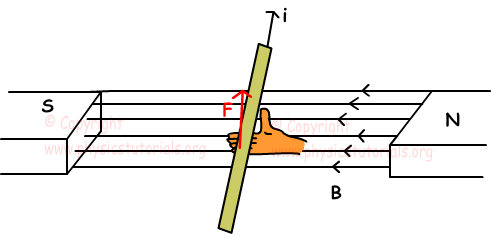 If the angle between the current and magnetic field ß;
If the angle between the current and magnetic field ß;
1. ß=0 then sinß=0, F=0
2. ß=180 then sinß=0, F=0
3. ß=90 then sinß=1, F=B.i.l
We can say that, if the direction of current and magnetic field are parallel to each other then, no force exerted on the wire.
Example: Which one of the magnetic force acting on the wires is/are zero given in the picture below?
 Since the directions of the currents i₁ and i₂ are parallel to the direction of magnetic field, no force exerted on these currents. F₁=F₂=0
Since the directions of the currents i₁ and i₂ are parallel to the direction of magnetic field, no force exerted on these currents. F₁=F₂=0
i₃ current is perpendicular to the magnetic field thus,
F₃=B.i₃.l
Direction of the magnetic force is toward us.
Example: Find the directions of the magnetic forces acting on the currents i₁, i₂ placed in a constant magnetic field.
 Magnetic forces acting on the currents i₁ and i₂ are shown in the picture below.
Magnetic forces acting on the currents i₁ and i₂ are shown in the picture below.
 Force Acting on Charged Particle
Force Acting on Charged Particle
Force acting on a current is explained above. We have learned that current is produced by the motion of charged particles. Thus, force on current carrying wire is the sum of forces acting on each charged particle which this current. If the particle has charge q, velocity v and it is placed in a magnetic field having strength B force acting on this particle and ß is the agle between the velocity and magnetic field is found with following formula;
F=q.v.B.sinß
 If;
If;
1. v=0, then F=0 no force exerted on stationary particle in magnetic field.
2. ß=0, then sin0=0 and F=0
3. ß=180, then sin180=0, and F=0, magnetic field lines and velocity of particle parallel to each other, then no force exerted on it.
4. ß=90, then sin90=1, F=q.v.B
Forces of Currents Carrying Wires on Each Other
 Experiments done on this subject shows that currents in the same direction attract each other since they produce opposite magnetic fields. On the contrary currents in opposite directions repel each other since they produce magnetic fields having same directions. We find the force exerted on each of them with following formula,
Experiments done on this subject shows that currents in the same direction attract each other since they produce opposite magnetic fields. On the contrary currents in opposite directions repel each other since they produce magnetic fields having same directions. We find the force exerted on each of them with following formula,
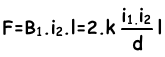 Where; l is the length of the wires, d is the distance between them.
Where; l is the length of the wires, d is the distance between them.