Magnetism Exam 2 and Problem Solutions

1.

a) Find whether the transformer is step down or step up.

b) Find V₁/V₂

c) Find whether secondary voltage depends on R or not. Magnetism a) Since the number of turns in primary side is larger than the secondary side, transformer is step down.

b) V₁/V₂=NA/NB=5N/N=5

c) V₁/V₂=NA/NB

V₁=V₂.NA/NB

Thus, V₁ does not depend on resistor R.

2. If the system given below is in equilibrium, find the poles of magnets. Magnetism B attracts C and repels A. Thus;

If B is N, then C must be S and A must be N

If B is S, then C must be N and A must be S

3. Force F acting on the AC wire, placed in a magnetic field B, is shown in the picture. Find the force acting on CB wire having length L. Magnetism We find direction of force by right hand rule.

Direction of force is outward.

FAC=B.I.2L=F

FCB=B.2I.L=F

So, force acting on CB wire has magnitude F and, it is in -X direction.

4. Three wires A, B and C are given below. If force acting on the one part of B exerted by A is F. Find resultant forces acting on wire C. 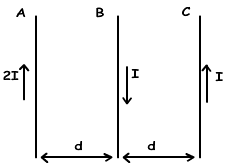Magnetism Since directions of currents on A and B are opposite in directions, A repels B.

FAB=2k.(2I.I/d).L=F

A attracts C, B repels C

FAC=2k.(2I.I/2d).L

FBC=2k.(I.I/d).L

FAC=FBC

Resultant force acting on C is zero.

5. If the magnetic field at point O is zero, find the ratio of r₁/r₂. Magnetism Magnetic field of circle having radius r₁;

B₁=1/2.(2π.k.I/r₁) inward

Magnetic field of circle having radius r₂;

B₂=1/4.(2π.k.I/r₂) outward

Since resultant magnetic field at point O is zero;

B₁=B₂

1/2.(2π.k.I/r₁)=1/4.(2π.k.I/r₂)

r₁/r₂=2