Relative Motion
When we talk about the velocity of something we first determine a reference point and then according to this reference point we say the velocity of the object. For example, you are in a bus and it goes with the velocity of 50 m/s to the east, then a truck passes you with a velocity of 60m/s to the east. When the truck is next to the bus you feel that as you go backward to the west or when the two cars have same velocity when you look another car you feel you do not move. On the contrary, consider the below examples, if you look at the stationary objects at the ground when you travel, then you feel yourself travel with the velocity of the car. All these are the result of relative motion. Velocity of the moving objects with respect to other moving or stationary object is called “relative velocity” and this motion is called “relative motion”. Reference point is too important in physics. We do all calculations according to the reference points. For instance, we observe the plane flying in the air, velocity of that plane with respect to us is the sum of the velocities of plane and the wind. However, the same plane has different velocity with respect to the flying other plane. To sum up, we determine the directions and quantities of velocity of the objects with respect to a chosen reference point. We look at some examples and vector notations of relative velocity of the objects.
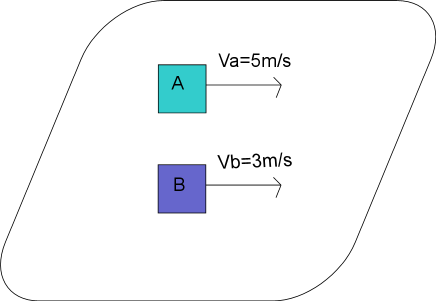
 In the first picture according to the observer in A, B is traveling with the velocity of 2m/s to the west. However, according to the observer in B, A is traveling with the velocity of 2m/s to the east.
In the first picture according to the observer in A, B is traveling with the velocity of 2m/s to the west. However, according to the observer in B, A is traveling with the velocity of 2m/s to the east.
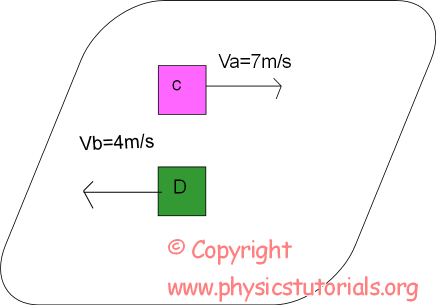
In the second picture observer in C feels that as if they are traveling with a velocity of 11m/s to the east with respect to D. On the contrary, observer in D feels that as if they are traveling with a velocity of 11m/s to the west with respect to C.
Now, I give you an equation which helps you to find relative velocities of the objects.
Vrelaltive=Vobject-Vobserver
Example: What is the velocity of the B with respect to A?
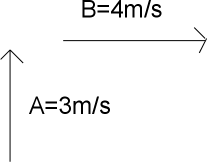
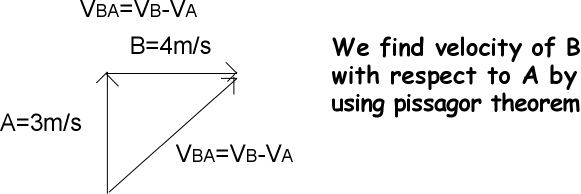 V²BA=V²B+V²A
V²BA=V²B+V²A
V²BA=3²+4²
V²BA=25
VBA=5m/s to the southeast
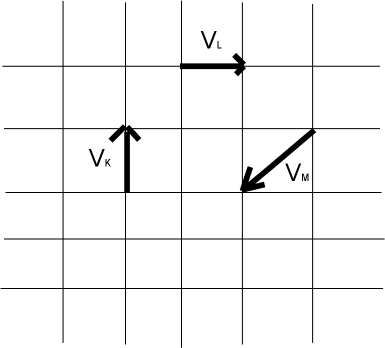
Example: Find the velocity of L with respect to K and M.