Impulse
We discussed above the factors changing momentum which are mass and velocity. In most of the case mass is constant and for momentum change velocity changes. If velocity changes then acceleration occurs. In the first unit we said that force causes acceleration in other words change in the velocity is the result of applied net force. Change in the velocity is proportional to the applied net force. If it is big then change is also big. Another important thing is the time of applied force. How long does it act on an object? It is linearly proportional to the change in velocity. If you apply a force on an object 1 s then you see small change in the momentum. However, if you apply force on an object long period of time then you see the amount of change in momentum is bigger than the first situation. In summary, I try to say that impulse is the multiplication of applied force and time interval it applied. Impulse is also a vector quantity having both magnitude and direction. It has the same direction with applied net force.
Impulse=Force.Time Interval
Impulse and momentum are directly related to each other. Let’s find this relation now.
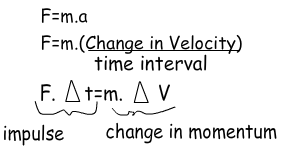As you can see, we found that impulse is equal to the change in momentum. In examples we will benefit from this equation.
Impulse=Change in Momentum
Example: If the time of force application is 5s find the impulse of the box given below.
Impulse=Force.Time Interval
Impulse=15N.5s
Impulse=75N.s
Example: Find applied force which makes 10m/s change in the velocity of the box in 5s if the mass of the box is 4kg.
Impulse=Change in momentum
F.t=p2-p1
F.t=m. (V2-V1)
F.t=4kg.10m/s=40kg.m/s Impulse of the box is 40kgm/s
F=40kg.m/s/5s=8N Applied force
We experience the results of impulse and momentum in daily life. For example, in collisions like car crash or any other collision we can calculate the affect of force by controlling the time. Assume that, you push a box with a force of 10N for 2 seconds, the impulse is 20N.s. Then you push it with a 5N force for 4 seconds and impulse does not change. As you see increasing the time decreases the amount of force. Thus, the unwanted results of force can be eliminated by increasing the time of force application. On the contrary if you want big force then you should decrease the time and you get big force.
In this unit we will again benefit from the graphs. Look at the given graph below that shows the relationship of the force and time of a given system.
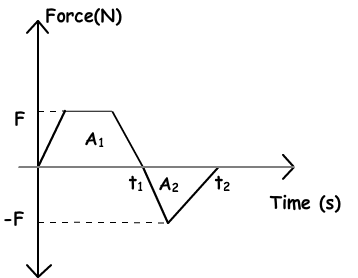Since impulse is equal to the multiplication of force and time then, area under this graph also gives us impulse. As shown in the graph, A1 is positive impulse and A2 is negative impulse. Total impulse gives us the change in momentum as we said before.
We can also draw momentum versus time and velocity versus time graph of the system.
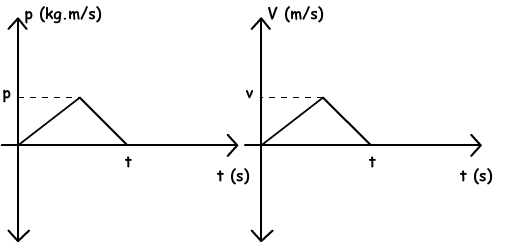As you can see momentum vs. time graph and velocity vs. time graphs of the system are similar because momentum is directly proportional to the velocity.
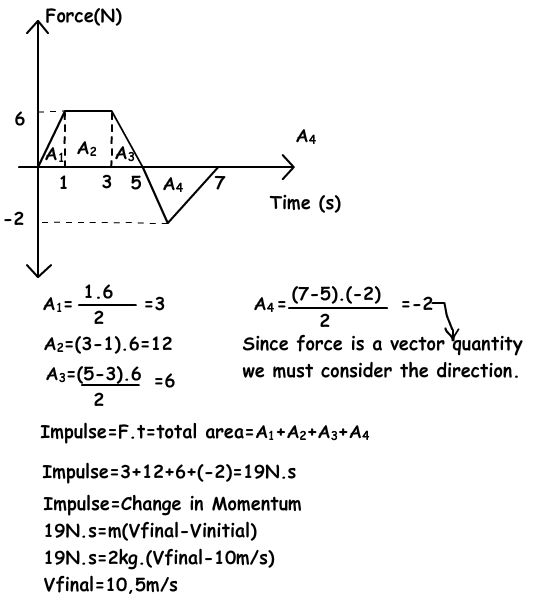
Example: The graph given below belongs to an object having mass 2kg and velocity 10m/s. It moves on a horizontal surface. If a force is applied to this object between (1-7) seconds find the velocity of the object at 7. Second.
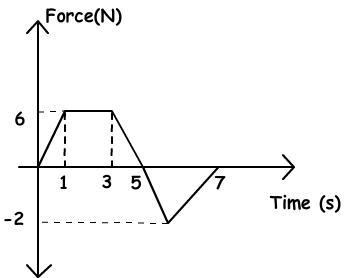Area under the graph gives us impulse. First, we find the total impulse with the help of graph given above then total impulse gives us the momentum change. Finally, we find the final velocity of the object from the momentum change.
