Properties of Matter Exam 1 and Problem Solutions

1. Three different tubes are filled with same liquid having density d₁. If the rest of the tubes are filled with another liquid having density d₂, find the relation between the densities of the liquids in the tubes. (d₂>d₁) Heights of three tubes are equal, thus liquids mixed in the tubes have same volume. Densities of the liquids become;

d₁=d₂=d₃

2. Mass vs. volume graph of two liquid is given below. If we take 160g X water and 40 cm³ from Y water, find the density of homogeneous mixture. Using graph given above;

dx=80/20=4g/cm³

dy=40/20=2g/cm³

dmixture=(mx+my)/(Vx+Vy)

dmixture=(mx+Vy.dy)/mx/dx+Vy

dmixture=(160+40.2)/160/4+40

dmixture=3g/cm³

3. We mix two different liquids having equal volumes and densities d₁=0,8 g/cm³ and d₂=d. If final density of the mixture is 1,2g/cm³, find the density of second liquid.

If the volumes of matters are equal we use following formula to find density of mixture;

dmixture=(d₁+d₂)/2

1,2=(0,8+d)/2

2,4-0,8=d

d=1,6g/cm³

4. Flow rates of two tap are equal and liquids have densities 3d and d. These two taps fill the half of the tank shown in the picture given below and rest of the tank is filled by the tap having liquid density d. Draw the density vs. time graph of the liquid in the tank. Since the flow rates of two taps are equal, density of the mixture in first half is;

dmixture1=3d+d/2=2d

Rest of the tank is filled by the tap having liquid density d. So, final density of the mixture becomes;

dmixture2=2d+d/2=1,5d

Density vs. time graph of mixture is; 5. A prism made of matter having density 5 g/cm³, has mass 600g. Find the volume of the space inside the prism. 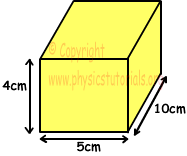Exterior volume of the prism is;

Vexterior=4.5.10=200cm³

Volume of the matter used for prism=600/5=120cm³

Thus;

Volume of the space inside prism is=200-120=80cm³