Work Power Energy Exam 3 and Problem Solutions

1. A box is released from point A and it passes from point D with a velocity V. Works done by the gravity are W₁ between AB, W₂ between BC and W₃ between CD. Find the relation between them. Work done by gravity is equal to change in potential energy of the object.

Interval AB: W₁=ΔEp=-mgh

Interval BC: W₂=ΔEp=-mgh

Interval CD: W₃=ΔEp=0

W₁=W₂>W₃

2. An object thrown with an initial velocity V from point A. It reaches point B and turns back to point A and stops. Find the relation between the kinetic energy object has at point A and energy lost on friction. Object has kinetic energy at point A;

EK=1/2.mV²

Object stops at point A, which means that all energy is lost on friction.

EK=Efriction

3. We throw object from point A with an initial kinetic energy E, and it reaches point C. How much energy must be given to make object reach point D. Using conservation of energy theorem;

E=2mgh+Ffriction.2X

E=2(mgh+Ffriction.X)

mgh+Ffriction.X=E/2

E’=3mgh+Ffriction.3X

E’=3(mgh+Ffriction.X)

E’=3.E/2=1,5E

we must give 1,5 E energy to make object reach point D.

4. 3 rectangular plates are hanged as shown in the figure given below. If the masses of the plates are equal, find the relation between the potential energies of the plates. 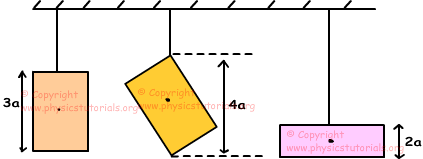Masses of the plates are equal but center of masses are different.

EP₁=m.g.3a/2

EP₂=m.g.2a

EP₃=m.g.a

EP₂ >EP₁ > EP₃

5. System given below is in equilibrium. If the potential energies of objects A and B are equal, find the mass of object A in terms of G. (Rod is homogeneous and weight of it is G.) Since rod is homogeneous we can take weight of it at the center.

Equal potential energies;

GA.4h=GB.h

GB=4GA.

Moment of the system;

GA.3+G.1=GB.1

3GA+G=4GA

GA=G