Potential Energy
Objects have energy because of their positions relative to other objects. We call this energy as potential energy. For example, apples on the tree, or compressed spring or a stone thrown from any height with respect to ground are examples of potential energy. In all these examples there is a potential to do work. If we release the spring it does work or if we drop the apples they do work. To move the objects or elevate them with respect to the ground we do work. The energy of the objects due to their positions with respect to the ground is called gravitational potential energy.
 The pictures given above are the examples of gravitational potential energy. They both have a height from the ground and because of their positions they have energy or potential to do work. Look at the given examples below. They are a little bit different that of given above.
The pictures given above are the examples of gravitational potential energy. They both have a height from the ground and because of their positions they have energy or potential to do work. Look at the given examples below. They are a little bit different that of given above.

 In the first picture, system including a spring and a box is at rest. However, in second picture the box compresses the spring and loads it with potential energy. If we release the box spring does work and pushes the box back. These two examples of gravitational and spring potential energy are calculated differently. Let me begin with the calculation of gravitational potential energy. We will look at which factors effects the magnitude of potential energy or which does not effect. Work done against to the earth to elevate the objects is multiplication of its weight and distance which is height. Thus, as we said before energy is the potential of doing work.
In the first picture, system including a spring and a box is at rest. However, in second picture the box compresses the spring and loads it with potential energy. If we release the box spring does work and pushes the box back. These two examples of gravitational and spring potential energy are calculated differently. Let me begin with the calculation of gravitational potential energy. We will look at which factors effects the magnitude of potential energy or which does not effect. Work done against to the earth to elevate the objects is multiplication of its weight and distance which is height. Thus, as we said before energy is the potential of doing work.
Then, gravitational potential energy becomes;
PE=mg.h
Now, look at the given picture and try to calculate the potential energies of the given ball in three situations.
 We see that gravitational potential energy depends on the weight and height of the object. Now let’s solve some more examples related to this topic before passing to the kinetic energy.
We see that gravitational potential energy depends on the weight and height of the object. Now let’s solve some more examples related to this topic before passing to the kinetic energy.
Example: In the pictures given below, if the potential energy of the ball in the first picture is P find the potential energy of the ball in second situation in terms of P.
 Situation1
Situation1
P=m.g.h=mgh
Situation2
P’=m.g.2h=2mgh=2P
POTENTIAL ENERGY OF THE SPRING
By compressing the spring or stretching it you load a potential energy to it. Well, if I apply same force to different springs having different thicknesses, are they loaded with the same energy? I hear that you all say no! You are absolutely right. Of course the thinner spring is more compressed than the thicker one where the quantity of compression shows the loaded potential energy. What I want to say is that, potential energy of the spring depends on the type of spring and the amount of compression. The mathematical representation of this definition is given below.
Ep=1/2.k.x²
Where k is the spring constant and x is the amount of compression.
 Now, we look at the origin of this formula. This is a picture of a spring at rest. There is no compression or stretching. Thus, we can not talk about the potential energy of the spring. However, in the pictures given below springs are not at rest position. Let’s examine the behavior of the springs in two situations.
Now, we look at the origin of this formula. This is a picture of a spring at rest. There is no compression or stretching. Thus, we can not talk about the potential energy of the spring. However, in the pictures given below springs are not at rest position. Let’s examine the behavior of the springs in two situations.
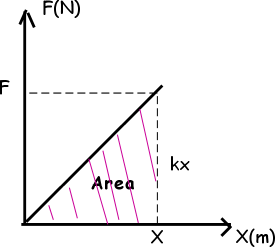
 In the first picture, we apply a force, Fapplied, and spring reacts this force with Fspring=-kx. The amount of compression is X. In the second picture we stretch the spring by the amount of X. We apply force of F and spring gives reaction to this force with Fspring=-kx where x is the stretching amount and k is the spring constant. The given graph below is force versus distance graph of springs. We find the energy equation of spring by using this graph.
In the first picture, we apply a force, Fapplied, and spring reacts this force with Fspring=-kx. The amount of compression is X. In the second picture we stretch the spring by the amount of X. We apply force of F and spring gives reaction to this force with Fspring=-kx where x is the stretching amount and k is the spring constant. The given graph below is force versus distance graph of springs. We find the energy equation of spring by using this graph.
As I said before area under the force vs distance graph gives us the work and energy is the capability of doing work. So, area under this graph must give us the potential energy of the spring.
Area=1/2.F.x=1/2.kx.x=1/2kx²
Ep=1/2kx²
Example: 50N of force is applied to a spring having 150N/m spring constant. Find the amount of compression of the spring.
 Fspring=-kx=Fapplied
Fspring=-kx=Fapplied
50N=-150.x
X=-3m “-“ shows the direction of compression.