Angular Acceleration
Look at the given picture above. The speed of the system is constant and we show it with “v”.
 However, as you can see direction of the speed changes as time passes and always tangent to the circle. Change in the direction of velocity means system has acceleration which is called angular acceleration. Since the acceleration is;
However, as you can see direction of the speed changes as time passes and always tangent to the circle. Change in the direction of velocity means system has acceleration which is called angular acceleration. Since the acceleration is;
a = (Vf-Vi)/t
Direction of the acceleration is same as the direction of change of velocities.
 We should find the direction of the changes in the velocity by using vector properties. Let’s show how we find the direction of acceleration. Picture shows the change in the direction of velocity. AS you can see direction of the resultant velocity vector is towards to the center of the circle. Because of the direction of acceleration, we call it centripetal acceleration.
We should find the direction of the changes in the velocity by using vector properties. Let’s show how we find the direction of acceleration. Picture shows the change in the direction of velocity. AS you can see direction of the resultant velocity vector is towards to the center of the circle. Because of the direction of acceleration, we call it centripetal acceleration.
Mathematical representation of centripetal acceleration is;
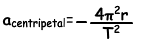 “-“sign in front of the formula shows the direction with respect to the R position vector.
“-“sign in front of the formula shows the direction with respect to the R position vector.
We can rewrite centripetal acceleration in terms of angular velocity and tangential velocity.
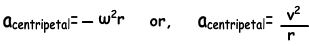 Example: If the tangential speed of the object is 3m/s which is doing circular motion on a path of radius 2m, find the centripetal acceleration of it.
Example: If the tangential speed of the object is 3m/s which is doing circular motion on a path of radius 2m, find the centripetal acceleration of it.
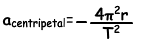 Or we can rewrite it as;
Or we can rewrite it as;
a=V²/r=(3m/s)²/2m=4,5m/s²